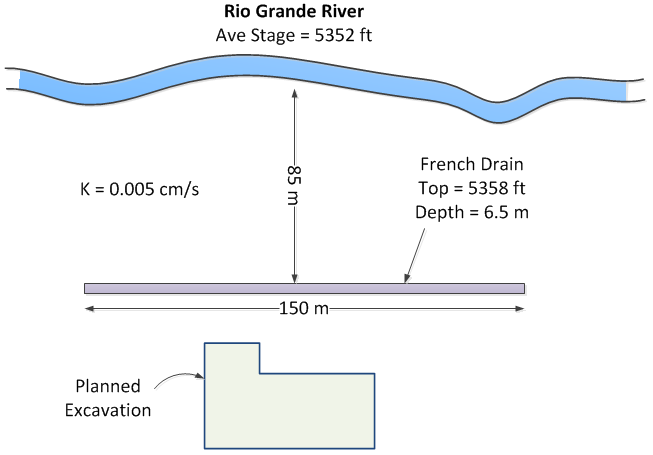
1) The Los Pollos Hermanos Corporation is planning to build a new manufacturing facility near the Rio Grande River in the outskirts of Albuquerque, New Mexico. The facility will include a hermetically-sealed underground unit with state-of-the-art ventillation and chemical-processing equipment. In order to dewater the site during construction and to ensure that it stays dry while in operation, the company decides to build a french drain between the river and excavation as follows:

A pump will be attached to the drain and the water will be returned to the river. Calculate what capacity will be required (gpm) for the pump. To simplify your calculations, assume that there is a lower permeability layer at the elevation corresponding to the bottom of the excavation. Use a spreadsheet for your calculations.
NOTE: Be careful with the values for Ho and HD in the equation. They should be measured from the datum, which is the bottom of the trench. Don't use the elevations.
2) You client decides that the french drain is too expensive so you have been asked to design a dewatering system for the same site using a set of wells placed near the excavation. To do the design, we will use the multi-well spreadsheet we developed in class to solve a construction dewatering problem. The region marked with bold lines represents the boundary of a proposed excavation. You should determine how many wells to use, what pumping rate will be required, and where the wells should be located. To facilitate the excavation process, assume that that wells must be placed at least one cell width (10 m) away from the excavation:
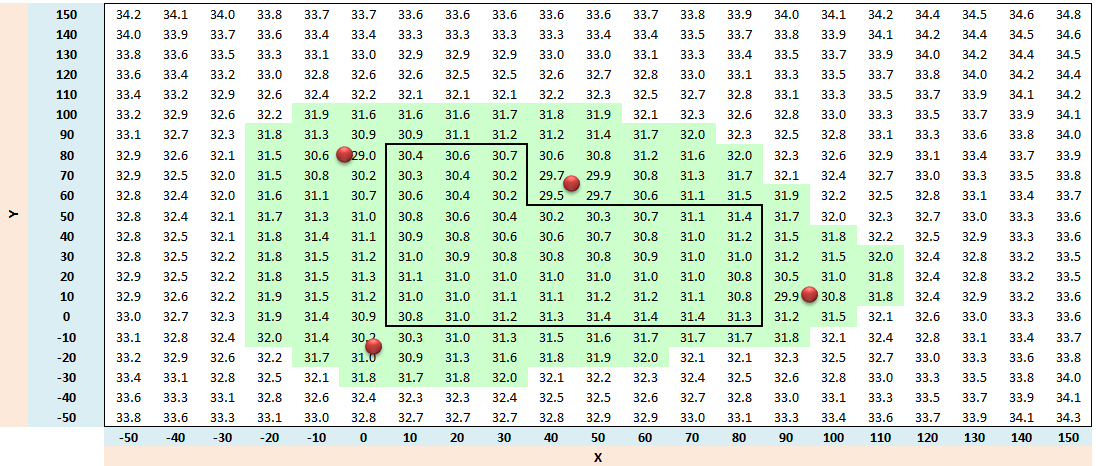
Use the following inputs as you solve the problem:
k = 0.005 cm/s
R = 500 m
Elevation of ground surface = 5358 ft
Depth of excavation = 8 m
For this case, assume that there is a lower permeability later at a depth of about 40 m from the ground surface. The excavation depth is relative to the initial ground surface. Use the elevation of the river for your initial water table elevation.
Repeat the design using 1, 2, 3, 4, 5, and 6 wells. For each case, experiment to find the best location for the well(s) and the required pumping rate. Put your results in a Word document. Include a table showing Q vs. number of wells and include a screen shot of each of your six configurations. Also make a few comments on what you learned as a result of the exercise (including which design you would select).
Tip: You may want to try using the Excel Solver. Once you have a configuration of well locations, it can be used to find the Total Q that optimally solves the dewatering condition. Have it maximize the max head value by altering total Q subject to the constraint that the max head should be less than or equal to the design head.
Zip up the spreadsheed from part (1) and the Word document from part (2) into a single zip archive. Upload your zip archive via Learning Suite.